File Information
Library: Geo
Package: Geo
Header: Poco/Geo/LatLon.h
Description
LatLon represents a point on the two-dimensional surface of a globe. Latitude is the degrees North and ranges between [-90, 90] while longitude refers to degrees East, and ranges between (-180, 180].
Based on code from the LatLon (gov.nasa.worldwind.geom.LatLon) class from the NASA World Wind Java source code released under the NOSA license.
Note: when comparing LatLons for equality, the usual issues when comparing floating-point numbers should be considered.
Member Summary
Member Functions: assign, equals, fromDegrees, fromRadians, greatCircleAzimuthTo, greatCircleDistanceTo, greatCircleEndPosition, latitude, longitude, operator !=, operator =, operator ==, rhumbAzimuthTo, rhumbDistanceTo, rhumbEndPosition, swap
Constructors
LatLon
LatLon();
Creates a zero LatLon.
LatLon
LatLon(
const LatLon & other
);
Creates a LatLon by copying another one.
LatLon
LatLon(
const Angle & latitude,
const Angle & longitude
);
Creates a LatLon with the given latitude and longitude.
Destructor
~LatLon
~LatLon();
Destroys the LatLon.
Member Functions
assign
void assign(
const LatLon & other
);
Assigns another LatLon.
assign
void assign(
const Angle & latitude,
const Angle & longitude
);
Assigns another latitude and longitude.
equals
bool equals(
const LatLon & other,
double delta
) const;
Returns true if the other position is within the given delta of this position. Delta is given in degrees.
fromDegrees 
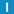
static LatLon fromDegrees(
double latitude,
double longitude
);
Creates a LatLon from the given latitude and longitude in degrees.
fromRadians 
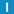
static LatLon fromRadians(
double latitude,
double longitude
);
Creates a LatLon from the given latitude and longitude in radians.
greatCircleAzimuthTo
Angle greatCircleAzimuthTo(
const LatLon & latLon
) const;
Computes the azimuth angle (clockwise from North) that points from this location to the second location using the harvesine formula.
This angle can be used as the starting azimuth for a great circle arc that begins at the first location, and passes through the second location.
greatCircleDistanceTo
Angle greatCircleDistanceTo(
const LatLon & latLon
) const;
Computes the great circle angular distance between two locations using the harvesine formula.
The return value gives the distance as the angle between the two positions on the PI radius circle. In radians, this angle is also the arc length of the segment between the two positions on that circle. To compute a distance in meters from this value, multiply it by the radius of the globe.
Example: compute the distance (in meters) between New York and San Francisco:
LatLon sanFrancisco(LatLon::fromDegrees(37.728965, -122.420151)); LatLon newYork(LatLon::fromDegrees(40.712180, -73.995796)); Angle a = newYork.greatCircleDistanceTo(sanFrancisco); double m = a.radians()*LatLon::EARTH_MEAN_RADIUS;
greatCircleEndPosition
LatLon greatCircleEndPosition(
const Angle & greatCircleAzimuth,
const Angle & arcDistance
) const;
Computes the location on a great circle arc with this as starting location, the given azimuth, and arc distance.
To compute the arcDistance (in radians) from a distance in meters, divide the distance in meters by the radius of the globe.
Example: travel from New York to San Francisco (distance: 4131767 meters, heading: 281.6 degrees)
LatLon newYork(LatLon::fromDegrees(40.712180, -73.995796));
LatLon destination = newYork.greatCircleEndPosition(Angle::fromDegrees(281.6),
Angle::fromRadians(4131767.0/LatLon::EARTH_MEAN_RADIUS));
latitude 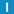
const Angle & latitude() const;
Returns the latitude.
longitude 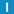
const Angle & longitude() const;
Returns the longitude.
operator != 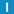
bool operator != (
const LatLon & other
) const;
operator =
LatLon & operator = (
const LatLon & other
);
Assignment operator.
operator == 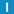
bool operator == (
const LatLon & other
) const;
rhumbAzimuthTo
Angle rhumbAzimuthTo(
const LatLon & latLon
) const;
Computes the azimuth angle (clockwise from North) of a rhumb line (a line of constant heading) between two locations.
rhumbDistanceTo
Angle rhumbDistanceTo(
const LatLon & latLon
) const;
Computes the length of the rhumb line (a line of constant heading) between two locations.
The return value gives the distance as the angular distance between the two positions on the PI radius circle. In radians, this angle is also the arc length of the segment between the two positions on that circle. To compute a distance in meters from this value, multiply it by the radius of the globe.
rhumbEndPosition
LatLon rhumbEndPosition(
const Angle & rhumbAzimuth,
const Angle & arcDistance
) const;
Computes the location on a rhumb line with the given starting location, rhumb azimuth, and arc distance along the line.
To compute the arcDistance (in radians) from a distance in meters, divide the distance in meters by the radius of the globe.
swap
void swap(
LatLon & other
);
Swaps the LatLon with another one.
Variables
EARTH_EQUATORIAL_RADIUS 
static const double EARTH_EQUATORIAL_RADIUS;
Earth equatorial radius in meters (6378137.0 m, derived from WGS-84 ellipsoid)
EARTH_MEAN_RADIUS 
static const double EARTH_MEAN_RADIUS;
Earth mean radius according to IUGG in meters (6371009 m)
EARTH_POLAR_RADIUS 
static const double EARTH_POLAR_RADIUS;
Earth polar radius in meters (6356752.3 m, derived from WGS-84 ellipsoid)
ZERO 
Zero LatLon (for Earth, the crossing of equator and Greenwich meridian)